文理フィフティフィフティ

　2月13日、文部科学省は、高校教育改革の基本方針を発表し、2040年に、公立高校の普通科で文系と理系の生徒の割合が同程度になるよう改革を進めることとした。今は、2026年だから、あと14年である。ということは、すでに2歳の子どもたちからということになる。本当にこのようなことができるのだろうか。

　できる、できないは別にして、理系人材が求められているのは確かだ。ＩＴ人材も不足しており、ＡＩ開発で世界から後れを取っている。高市首相もＡＩ産業に積極的に投資を行うことを表明している。世界の真ん中に日本がいようと思えば、科学技術に投資を行い、理系人材を増やすことが必須なのである。

　問題はそんなことができるのかということだ。足元の教育現場を見てみれば、どれだけ理系人材が育っているというのかということだ。高校では、現在2年生から文理分けが行われることが多いが、トップの進学校でも文：理＝５：５となっているところは少ないのではないか。大体は、文：理＝６：４というのが、平均的ではないだろうか。超難関進学校から段々と偏差値が下がるにつれて、文理の割合は文が増えて、理が減るというのが大体の傾向だ。中堅校になれば、文：理＝８：２ぐらいが相場である。これを一体どうやって普通科で文：理＝５：５にするというのだろうか。

　理系人材が育たない最も大きな原因は、算数・数学きらいが圧倒的だろう。理科も理系分野だが、そこには具体的な物が存在する。算数のもっとも簡単な「１＋１＝２」からして抽象化が始まっているのだ。
　「リンゴ1個とリンゴ1個でリンゴはいくつあるか？」
　「鉛筆1本と鉛筆1本で鉛筆は何本？」
という具体を捨象した世界が「１＋１＝２」なのである。この抽象化ということが算数・数学の最も大きな特徴なのである。これが数学の面白さであるのだが、また理解困難たらしめるところでもあるのだ。

　そうであるならば、どうすれば良いか。具体と抽象の往還を小学生高学年になっても、中学生になっても行うことが重要だ。数学が現実の社会とどのように結びつき、そして物事を解決しているかということに気づかせることである。
例えば、高校2年生で習う積分だが、微分を教えてからその逆演算として積分を教え、不定積分を学ぶ。そして、それが実は、面積を求めているのだということを後で教えるのだ。しかし、歴史的には、まずは定積分が発明されている。それが区分求積法である。区分求積法とは、下の図にあるように、面積を求めにくい曲線で囲まれた部分を、長方形で外側と内側で区切り、その長方形の幅を極限まで小さくしていけば、外からも内からも求めたい面積に近づくという考え方だ。

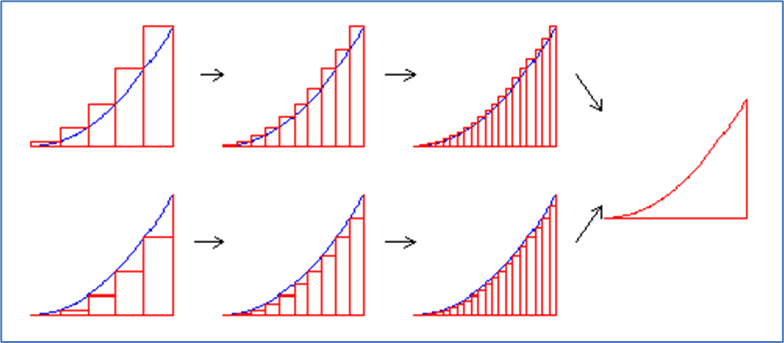
これを数式に表したのが、

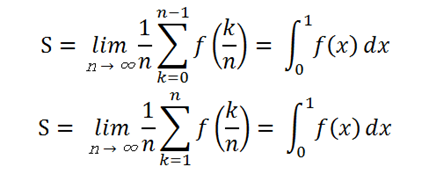
この式である。ところで、この抽象化された区分求積法を現実世界で活用している身近な機械をご存じだろうか。それは、コピー機である。光を当てて同じものを写し出すコピー機は、光という極めて小さい線を当てることにより長方形の極限を可能にしたのである。私は、高校生の時、この区分求積法を習ったが、感動したことを覚えている。

　今となっては、自分がどれだけ数学の才能が無いかは思い知らされているが、それでも数学の面白さは経験してきた。このような具体と抽象の往還を頻繁に行うことで、数学の面白さ、有益性が実感されるのではないだろうか。

　このようなことを行うためには、まだまだ教科書の内容も含め、大学入試の内容も含め、数学の授業時数も含め、数学教員の数も含め、改善しなければならないことが山ほどある。今年度中に答申がまとまる予定の2030年実施の次期学習指導要領は、2040年までの10年間のものである。ちょうど、文理フィフティフィフティにあたる学習指導要領なのだ。このような視点に立って、議論されているのだろうか。もう一度検証が必要である。